지난 시간까지 시간 복잡도 O(N ^ 2)인 선택 정렬, 버블 정렬, 삽입 정렬 알고리즘을 공부했습니다. 이어서 평균 시간 복잡도 O(N * logN)인 퀵 정렬에 대해서도 공부하는 시간을 가졌습니다. 이번 시간에 다룰 내용은 병합 정렬(Merge Sort) 입니다. 병합 정렬도 대표적인 '분할 정복' 방법을 채택한 알고리즘입니다. 결과적으로 퀵 정렬과 동일하게 O(N * logN)의 시간 복잡도를 가집니다.
다만 퀵 정렬은 피벗 값에 따라서 편향되게 분할할 가능성이 있다는 점에서 최악의 경우 O(N ^ 2)의 시간 복잡도를 가진다고 하였습니다. 병합 정렬은 정확히 반절씩 나눈다는 점에서 최악의 경우에도 O(N * logN)을 보장합니다. 개념 자체도 굉장히 쉽기 때문에 퀵 정렬을 이해하신 분들이라면 어렵지 않게 병합 정렬을 이해할 수 있을 겁니다.
병합 정렬은 하나의 큰 문제를 두 개의 작은 문제로 분할한 뒤에 각자 계산하고 나중에 합치는 방법을 채택합니다. 즉 기본 아이디어는 일단 정확히 반으로 나누고 나중에 정렬하는 것 입니다.
<TMI>
logN은 굉장히 작은 시간을 소요한다.
예를 들어,
2 ^ 10 = 1,000
2 ^ 20 = 1,000,000
log2N 에서 N이 1,000,000이라면 20밖에 안된다.
"일단 반으로 나누고 나중에 합쳐서 정렬하면 어떨까?"
예시를 통해서 알아보자.
병합 정렬은 퀵정렬과 다르게 피봇값을 기준으로 분할하지 않고, 항상 절반으로 동일하게 나눈다는 성질을 지니고 있습니다. 이러한 특징이 단계의 크기가 logN이 되도록 만들어줍니다.
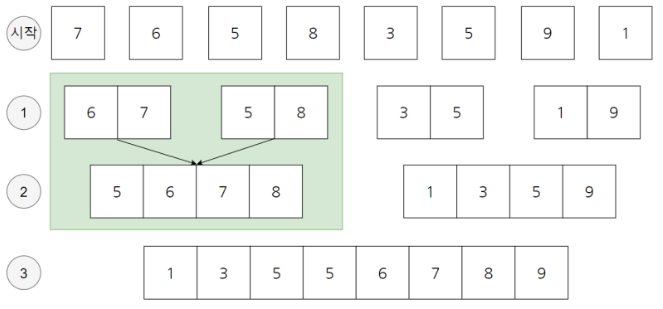
위 사진을 보면, 7 6 5 8 3 5 9 1 인 모두 크기가 개별 배열로, 즉 크기가 1인 배열 상태로 시작합니다. 이제 첫번째 1 단계에서는 각 배열의 크기가 2개입니다. 크기가1개였던 것들을 두 개씩 묶어서 합친 겁니다. 보시면 첫번째 1 단계에서는 67 / 58 / 35 / 19로 나누어진 것을 확인할 수 있습니다. 이어서 두 번째 단계는 크기가 2개였던 것들을 두 개씩 묶어서 크기가 4인 배열을 만듭니다.
다시 말해 합치는 순간에 정렬을 수행하는 겁니다. 합치는 단계는 오직 3단계면 됩니다. 합치는 겠수가 2배씩증가한다는 점에서 2^ 3 = 8이므로 3단계만 필요한 겁니다. 그러므로 단계의 크기는 데이티의 것수가 N개일때 logN을 유지하게 됩니다. 또한 정럴 자체에 필요한 수행 시간은 N입니다. 데이터의 갯수만큼만 연산하면 되기 때문이지요. 결과적으로 총 시간 복잡도는 O(N * logN)입니다.
단계가 log N이라는 것은 누구나 쉽게 이해찰 수 있을겁니다. 근데 왜 정렬에 필요한 수행시간이 N밖에 되지않는 것일까요? 부분 집합들을 정렬하는데 고작 N밖에안 드는 이유는 다음과 같습니다. 위 그림에서 초록색으로 색칠한 부분만 살펴보도록 합시다.
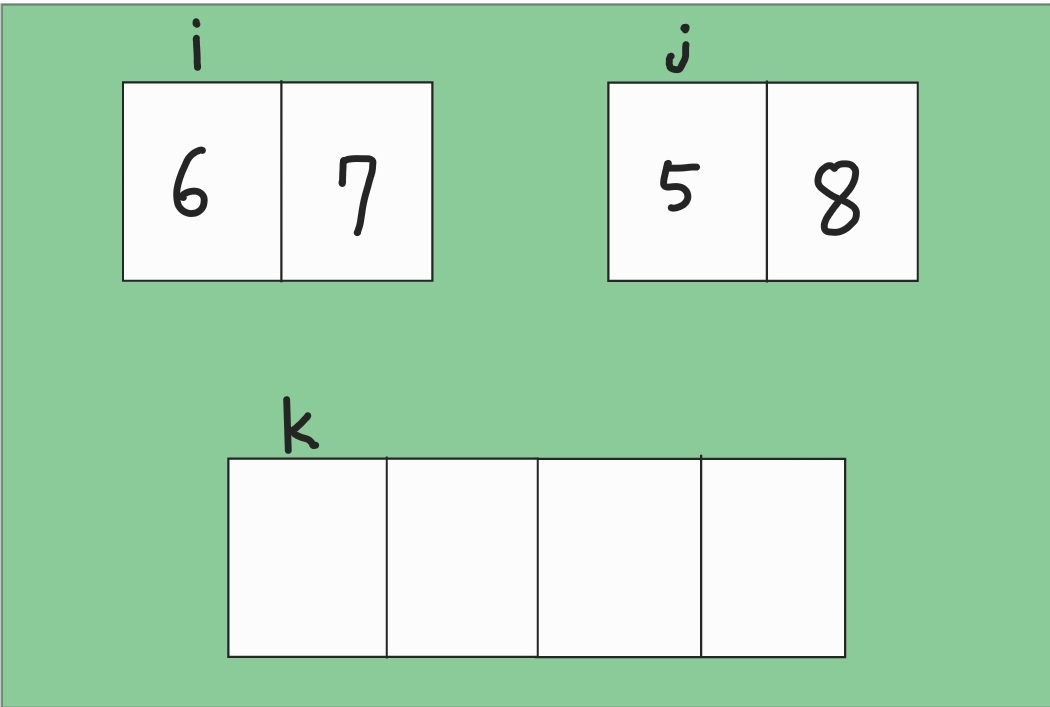
초기 상태는 위와 같습니다. 원쪽 집합에서는 i가 첫 번째 원소를 가리키고, 두 번째 집합에서는 j가 두 번째 원소를 가리키고 있습니다. 그리고 정렬될 배열은 비어있는상태입니다. 정럴에 N만 걸리는 이유는 삽입 정럴과 동일한 이유입니다, 바로 '부분 집합은 이미 정렬이 되어있는 상태'라고 가정하기 때문입니다. 이미 정렬이 되어있는 것 두 개 합치는 것은 시간 복잡도 O(N)이면 충분하기 때문입니다.

첫 번째 처리는 위와 같이 와 j를 비교해서 더 작은 숫자를 k의 위치에 넣고 처리한 인덱스를 1씩 더혜주는 겁니다. 그 결과 위와 같이 k, j가 한 칸 오른쪽으로 간 것을 알 수 있습니다.
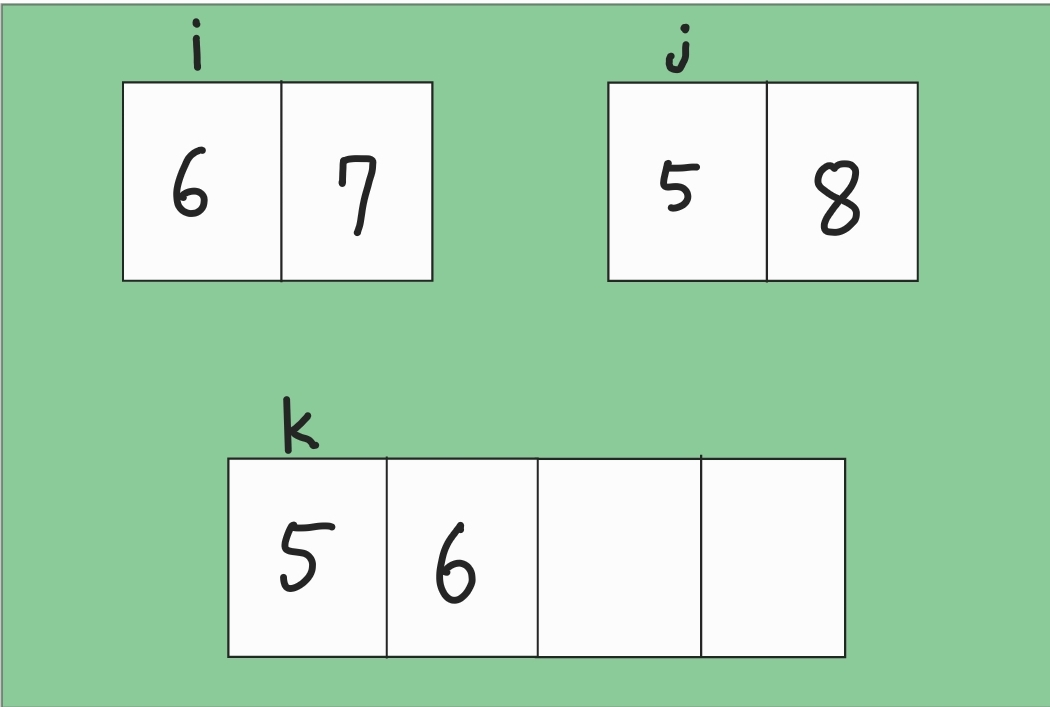
마찬가지로 i = 6과 j = 8를 비교해서 6이 더 작으므로 k의 위치에 십입하고 i, k를 각각 1씩 더해주는 겁니다. 그 결과는 위와 같습니다. 이런 식으로 반복하게 되면 정확히 N번만 처리하면 되는 것 입니다.

즉 위와 같이 너비가 N번, 높이가 log N번이므로 시간북잡도 O(N * logN)을 보장하는 것입니다. 이제 이 전체 과정을 소스코드로 작성하면 다음과 같습니다
"전체과정을 소스코드로 표현하면 다음과 같습니다."
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
int number = 8;
int sorted[8];
int size;
int count;
void merge(int a[], int m, int middle, int n) {
int i = m;
int j = middle + 1;
int k = m;
while (i <= middle && j <= n) {//작은 순서대로 배열에 삽입
if (a[i] <= a[j]) {
sorted[k] = a[i];
i++;
}
else {
sorted[k] = a[j];
j++;
}
k++;
}
if (i > middle) {//남은 데이터 삽입
for (int t = j; t <= n; t++) {
sorted[k] = a[t];
k++;
}
}
else {
for (int t = i; t <= middle; t++) {
sorted[k] = a[t];
k++;
}
}
for (int t = m; t <= n; t++) {//실제 배열에 데이터 옮기기
a[t] = sorted[t];
}
}
void mergeSort(int a[], int m, int n) {
if (m < n) {
int middle = (m + n) / 2;
mergeSort(a, m, middle);
mergeSort(a, middle + 1, n);
merge(a, m, middle, n);
}
}
int main() {
int array[8] = { 7,6,5,8,3,5,9,1 };
mergeSort(array, 0, number - 1);
for (int i = 0; i < number; i++) {
printf("%d ", array[i]);
}
}병합 정렬 코드를 구현할 때 신경 써줘야 하는 부분은 정렬에 사용되는 배열은 '전역 변수' 로 선언해 줘야 한다는 것입니다. 만약 함수 안에서 배열을 선언하게 된다면 매번 배열을 선언해 줘야하기 때문에 메모리 자원의 낭비가 매우 커질 수 있습니다. 이와 같이 기본적으로 병합정렬은 '기존의 데이터를 담을 추가적인 배열 공간이 필요하다'는 점에서 메모리의 활용이 비효율 적이라는 문제가 있습니다.
병합 정렬은 일반적인 경우 퀵정렬 보다 느리지만 어떠한 상황에서도 정확히 O(N * logN)를 보장할 수 있다는 점에서 몹시 효율적인 알고리즘 입니다.
'Algorithm' 카테고리의 다른 글
| 퀵정렬(QuickSort) (1) | 2023.07.23 |
|---|---|
| 알고리즘 Introduction & Analysis (0) | 2023.07.08 |
| Graph Algorithm(플로이드-워샬 알고리즘) (1) | 2023.03.02 |
| Graph Algorithm(벨만-포드 알고리즘) (0) | 2023.03.01 |
| Graph Algorithm(다익스트라 알고리즘) (0) | 2023.02.24 |
