플로이드-워샬(Floyd-Warshall) 알고리즘
모든 정점들간의 상호 최단거리(All Pairs Shortest Path)를 구하는 알고리즘이다.
응용 예시로는 Road Atlas, 네비게이션 시스템, 네트웍 커뮤니케이션 등이 있다. 그렇다면 플로이드-워샬이 무엇이고, 왜 쓰이는지 알아보자.
앞서 배운 다익스트라, 벨만-포드 알고리즘은 시작점이 주어지면 하나의 정점에서 다른 모든 정점으로의 최단경로를 구했다면, 플로이드-워샬 알고리즘은 모든 정점으로부터 모든 정점으로의 최단경로를 구하는대 사용된다.
알고리즘 구현 방식도 다르다. 다익스트라 알고리즘은 vertex set에서 가장 작은 노드를 꺼내서 하나씩 더하면서 최소값을 찾아가는 Greedy한 알고리즘을 사용하지만, 플로이드-워샬은 각 노드를 하나씩 선택해 전부 시작점이 되도록 설정한 뒤, 각 노드를 거쳐가는 모든 경로를 확인하는 알고리즘이다.
1. 다익스트라 알고리즘 수도코드 및 알고리즘 원리

① 반복문 : 다익스트라, 벨만포드 알고리즘은 시작점이 주어지고 시작점으로 부터의 최단경로만 구하면 되기 때문에 array의 형태지만, 플로이드-워샬은 모든 정점에서 모든 정점까지 다루므로 Metrix 형태로 나타내게 된다. 그래서 2중 for문으로 표현하고, 2차원 배열로 표현한다고 말할 수 있다.
② 반복문 : (2-1)은 거쳐가는 노드를 1부터 k까지 정해주는 반복문 이다. vertex의 집합으로 볼 수 있다.
(2-2)는 시작 정점을 의미하고, (2-3)은 마지막 정점을 의미한다.

vertex set에 속하는 것들만 거쳐 V1에서 Vj에 이르는 최단경로 길이를 의미한다.
","기준으로 앞에는 k를 포함하지 않은 거리, k를 포함한 거리로 나뉘게 된다.
따라서 두개 중 더 작은 값으로 갱신이 되는것인데 쉽게 표현하면, i→j와 i→k + k→j를 비교해주는 것이다.
2. 간단한 예시 그림으로 보기

1) 노드를 거쳐가지 않는 경우

k가 0일 때는 거쳐가는 노드가 0개라는 의미이다. 따라서 직접적으로 연결되 노드를 말하는 것이고, dº Metrix는 옆의 그림처럼 표현 된다. 자기 자신으로 가는 것을 당연히 0이 되고, 거쳐가는 가정을 하지 않았기 때문에 그래프 그대로 값을 넣어주면 된
다.
2) 노드 1을 거쳐가는 경우

k가 1일 때는 노드 1를 거쳐서 가는 경우에 최소비용을 계산해준다는 의미이다. 노드 1을 거쳐가는 경우에는 1이 포함되지 않는 않은 경우만 갱신이 가능하다. 1이 포함되지 않은 노드는 (2→3), (2→4), (3→2), (3→4), (4→2), (4→3) 총 6개의 노드가 있다. 그중에서 갱신이 가능한 노드는 (2→3)노드이다. 왜냐하면 노드를 갱신하기 위해서는 (2→3) > (2→1) + (1→3) 조건이 성립해야만 하기 때문이다. (2→3)의 값은 무한이였고, (2→1) + (1→3)의 값은 2여서 갱신이 됐다. 나머지는 조건을 만족하지 못해 갱신이 불가하다.
3) 노드 2를 거쳐가는 경우

k가 2일 때는 노드 2를 거쳐서 가는 경우에 최소비용을 계산해준다는 의미이다. 마찬가지로 2가 포함되지 않는 경우만 갱신이 가능하다. 자기 자신으로 가는 노드도 제외해 주어야 한다. 그중에서 갱신 조건이 충족하는 노드는 (4→1), (4→3) 이 된다. (4→1), (4→3)의 기존 값은 무한이였기 때문에 각각 3과 1로 갱신이 되었다.
4)노드 3을 거쳐가는 경우

2번과 3번처럼 계속해서 반복해주면 되는대, 이번에도 마찬가지로 노드3이 포함되지 않은 노드들 중에서 (1→4), (2→4)가 갱신이 가능한 것을 볼 수 있다. 기존의 값이 둘다 무한이였기 때문에 조건은 당연히 충족할 것이다.
5) 노드 4를 거쳐가는 경우
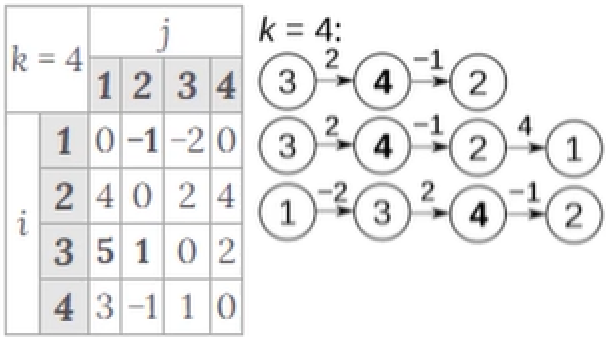
최종적으로 마지막 노드인 노드4를 거쳐가면 옆의 Metrix와 같이 모든 정점에서 모든 정점으로 가는 최소비용, 즉, 최단경로가 나오게 된다.
이러한 2차원 배열을 반복적으로 갱신하여 최종적으로 모든 최소 비용을 구해야 할 것이다. 바로 그러한 기준이 '거쳐가는 정점'인 것이다.
3. 플로이드 워샬 소스코드
#include <stdio.h>
int number = 4;
int INF = 10000000;
// 자료 배열을 초기화합니다.
int a[4][4] = {
{0, 5, INF, 8},
{7, 0, 9, INF},
{2, INF, 0, 4},
{INF, INF, 3, 0}
};
void floydWarshall() {
// 결과 그래프를 초기화합니다.
int d[number][number];
// 결과 그래프를 초기화합니다.
for(int i = 0; i < number; i++){
for(int j = 0; j < number; j++) {
d[i][j] = a[i][j];
}
}
// k = 거쳐가는 노드
for(int k = 0; k < number; k++) {
// i = 출발 노드
for(int i = 0; i < number; i++) {
// j = 도착 노드
for(int j = 0; j < number; j++) {
if(d[i][k] + d[k][j] < d[i][j]) {
d[i][j] = d[i][k] + d[k][j];
}
}
}
}
// 결과를 출력합니다.
for(int i = 0; i < number; i++) {
for(int j = 0; j < number; j++) {
printf("%3d ", d[i][j]);
}
printf("\n");
}
}
int main(void) {
floydWarshall();
}4. 수행시간
수행시간 : Θ(|V|³)
문제의 총수 Θ(|V|³), 각 문제의 계산에 Θ(1)
단점 : 시간이 오래걸리고, vertex가 많아질수록 case도 많아진다.
'Algorithm' 카테고리의 다른 글
| 퀵정렬(QuickSort) (0) | 2023.07.23 |
|---|---|
| 알고리즘 Introduction & Analysis (0) | 2023.07.08 |
| Graph Algorithm(벨만-포드 알고리즘) (0) | 2023.03.01 |
| Graph Algorithm(다익스트라 알고리즘) (0) | 2023.02.24 |
| 최단 경로(Shortest Paths) (0) | 2023.02.24 |
