다익스트라Dijkstra 알고리즘
다익스트라 최단 경로 알고리즘은 그래프에서 여러 개의 노드가 있을 때, 특정한 노드에서 출발하여 다른 노드로 가는 각각의 최단 경로를 구해주는 알고리즘이다. 다익스트라 알고리즘은 '음의 간선(0보다 작은 값을 가지는 간선)'이 없을 때 정상적으로 동작한다.
다익스트라 알고리즘은 프림 알고리즘 과 동작방식이 비슷하다. 다만 프림알고리즘은 단순히 간선의 길이를 이용해 어떤 간선을 먼저 연결할지 결정하는데 반해, 다익스트라 알고리즘은 '경로의 길이'를 감안해서 간선을 연결한다.다익스트라의 최단 경로 탐색 알고리즘은 사이클이 없는 방향성 그래프에 한해서만 사용 가능.
1. 다익스트라 알고리즘 수도코드 및 알고리즘 원리

S = r로부터의 거리가 계산되고 최단경로가 계산된 집합이다.
v = 모든 vertex에 대한 집합이다.
① for each u∈V모든 vertex에 대해서, d[u]를 무한대로 설정해준다. 즉 시작점으로 부터의 거리를 무한대로 해준다. 왜냐하면 아직 S에 포함이 되지 않았기 때문이다.d[r]을 시작점으로 잡고, 시작점을 0으로 설정해 준다.
② while(S≠V){}모든 Vertex에 대해서 r로부터의 거리가 계산이 되었다면 끝낸다. 조건에 만족하지 않는다면 S집합에 Vertex하나씩 추가해준다. u←extractMin(V-S,d); S집합에 포합되어있지 않는 V집합 중에서 d가 가장 작은 값을 u로 지정해준다. 이때 많은 사용자들이 extractMin을 구하기 위해서 for문을 사용하게 되는데 그렇게 되면 이중 for이 되어버려서 O(n²) 이 된다. 따라서 최소값을 구할 때는 우선순위 큐를 사용한 힙정렬을 사용해줘서 O(logn)이 될 수 있도록 한다. S←S ∪{u} 가장 작은 값을 S집합에 넣어준다.
③ for each v∈L(u) u로부터 연결되 정점들의 집합에 포합된 모든 vertex. 이 반복문이 이완(relaxation)해주는 부분이다.
④ if(v∈V-S and d[u] + w[u, v] < d[v]) then{} 아직 방문하지 않은 노드 와 d[u](현재 노드의 값)+w[u,v](현재노드와 다음 가르키는 노드의 간선 가중치의 값)이 d[v](다음 노드) 보다 작은 경우.
⑤ d[v] ← d[u] + w[u, v] 해당 vertex와 weight를 가르키는 다음 vertex의 값으로 update해준다.
⑥ prev[v]← u u에서 v가지 갔다고 표현해준다.
2. 그림으로 표현한 다익스트라 알고리즘

vertex안에 써있는게 전부 d이기 떄문에, 첫 번째 루프문이 돌게 되면 vertex 0이 r이 된다. 그래서 r이 0이 되고,
d = [ 0 ,∞ ,∞,∞...∞] 상태가 된다. 처음 vertex 0을 u(기준)을 잡고, 0과 인접한 노드는 ∞이고, 이완(relaxation)하면
[vertex 0 + weigt 8] > ∞ 니깐 인접한 노드가 업데이트하게 된다. 그렇게 인접한 노드들을 전부 반복해준다.

그 결과가 위의 그림이 된다. 이완된 노드에서 기준을 잡아야 하는데 이때 여기서, extractMin이 포함이 된다. 이미 S에 포함된 0을 빼고 본다면 vertex 8 이 된다.

vertex 8 이 u(기준)이 된다. 따라서 vertex 8은 S집합에 포함이 되고, u와 인접한 노드를 다시 이완(relaxation)시켜준다.
인접노드느 S에 포함되지 않고, [vertex 8 + weigt 10] > ∞ 이 성립하기 때문에 인접노드를 18로 업데이트 해준다.

다음으로 이완되어있는 노드 vertex 11, vertex 9, vertex 10 중에서 extartMin을 구하면 vertax 9가 되고, S에 포함시켜, u(기준)이 된다. 그리고 u와 인접한 노드를 다시 이완해주는데 vertex 9와 인접한 노드는 vertex 18, vertex 11이다.
vertex 19은 이완조건 [vertex 9 + weight 1] <18 에 성립하기 때문에 10으로 업데이트 해준다. 나머지 노드는 성립하지 않기 떄문에 그대로 놔둔다.
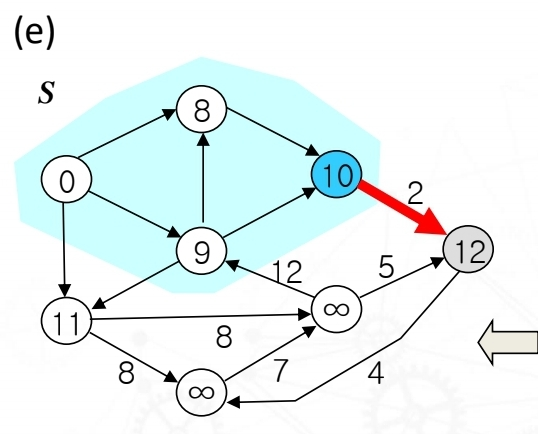
그리고 extractMin함수를 사용해서 10이 가장 작음으로 업데이트 된 노드 10을 S에 포함해주고 노드 10을 기준으로 잡는다. 노드 10과 인접한 노드는 하나 뿐이며 이완 조건에도 충족하므로 vertex 12로 업데이트해준다.
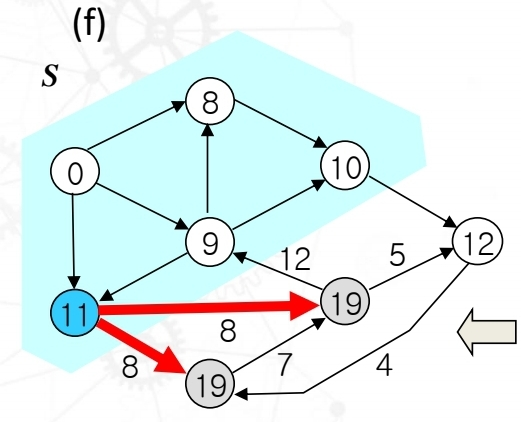
다음으로 인접한 노드중에서 가장 작은 vertex 11 을 S에 포함해주고 u로 잡는다. 그리고 인접한 노드들을 이완시켜준다.
위의 그림은 노드 11을 기준으로 잡고, 인접 노드를 이완해준 모습이다. 각각 vertex 19, vertex 19로 업데이트가 되었다.
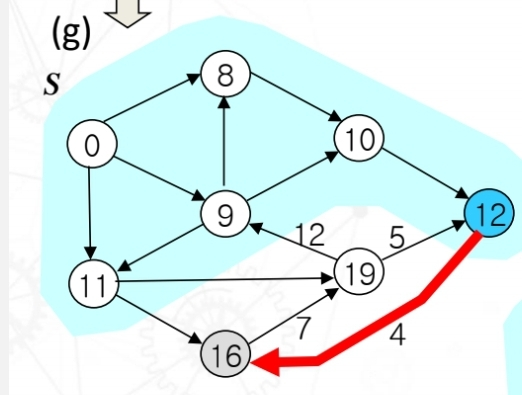
이제 다시하번 이완된 노드들 중에서 가장 작은 노드 12를 S에 포함해주고, 기준으로 잡아준다. 기준과 인접한 노드를 이완해주는데 이완 조건이 성립하게 된다. 따라서 vertex19에서 vertex16으로 업데이트 해준다.
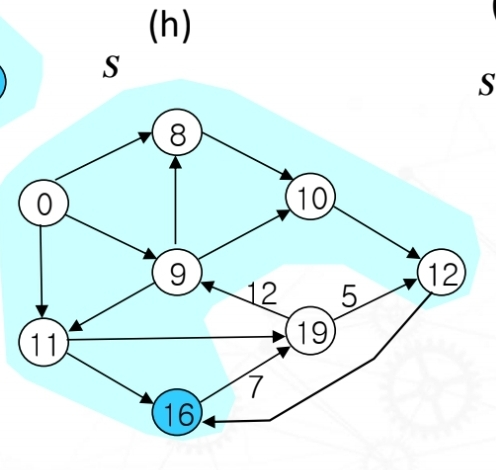
extractMin으로 노드16을 찾아주고, S에 포함시키면서 기준으로 잡아준다. 노드 16과 인접한 노드들을 이완하려 하지만 조건에 성립하는 노드가 없어서 건너뛰게 된다.
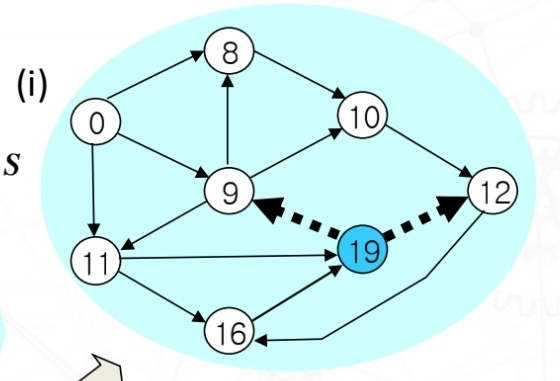
이제 마지막으로 S에 포함이 안된 노드19까지 S에 자동으로 포함시켜주면서 다익스크라 알고리즘은 마무리를 한다.
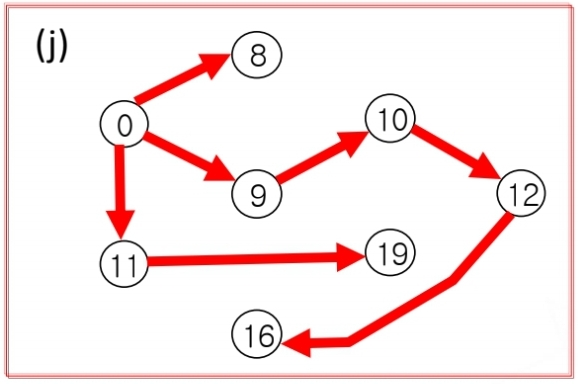
마무리 된 다익스트라 알고리즘의 최단 경로 이다.
3. 우선순위 큐(힙구조)를 이용한 다익스트라 알고리즘
#include<iostream>
#include<queue>
#include<vector>
using namespace std;
int INF = 1000000000;
int number =6 ;
vector<pair<int, int>>a[7];
int d[7];
void dijkstra(int start) {
d[start] = 0;
priority_queue<pair<int, int>>pq;
pq.push(make_pair(start, 0));
while (!pq.empty()) {
int current = pq.top().first;
int distance = -pq.top().second;
pq.pop();
if (d[current]<distance) continue;
for (int i = 0; i < a[current].size(); i++) {
int next = a[current][i].first;
int nextDistance = distance + a[current][i].second;
if (nextDistance < d[next]) {
d[next] = nextDistance;
pq.push(make_pair(next, -nextDistance));
}
}
}
}
int main(void) {
for (int i = 1; i <= number; i++) {
d[i] = INF;
}
a[1].push_back(make_pair(2, 2));
a[1].push_back(make_pair(3, 5));
a[1].push_back(make_pair(4, 1));
a[2].push_back(make_pair(1, 2));
a[2].push_back(make_pair(3, 3));
a[2].push_back(make_pair(4, 2));
a[3].push_back(make_pair(1, 5));
a[3].push_back(make_pair(2, 3));
a[3].push_back(make_pair(4, 3));
a[3].push_back(make_pair(5, 1));
a[3].push_back(make_pair(6, 5));
a[4].push_back(make_pair(1, 1));
a[4].push_back(make_pair(2, 2));
a[4].push_back(make_pair(3, 3));
a[4].push_back(make_pair(5, 1));
a[5].push_back(make_pair(3, 1));
a[5].push_back(make_pair(4, 1));
a[5].push_back(make_pair(6, 2));
a[6].push_back(make_pair(3, 5));
a[6].push_back(make_pair(5, 2));
dijkstra(1);
for (int i = 1; i <= number; i++) {
cout << d[i]<<" ";
}
}
'Algorithm' 카테고리의 다른 글
| Graph Algorithm(플로이드-워샬 알고리즘) (0) | 2023.03.02 |
|---|---|
| Graph Algorithm(벨만-포드 알고리즘) (0) | 2023.03.01 |
| 최단 경로(Shortest Paths) (0) | 2023.02.24 |
| Union-find Data Structure(트리를 이용한 처리) (0) | 2023.02.22 |
| Union-find Data Structure(연결 리스트를 이용한 처리) (0) | 2023.02.22 |
