트리를 이용한 처리
같은 집합의 원소들은 하나의 트리로 관리한다.
- 자식 노드가 부모 노드를 가리킨다.
트리의 루트를 집합의 대표 원소로 삼는다.
※연결 리스트와 차이점
1) 자식 노드가 대표노드가 아닌 부모노드를 가리킨다.
2) Binary 트리가 아니여서 자식도드를 여러개 가질 수 있다.
3) 연결 리스트에서 Find-Set(x)의 수행시간은 O(1)이였지만,
트리에서 수행시간은 트리의 depth(깊이)와 연관이 있다.
4) 연결 리스트는 대표노드를 가리키는 Point, 다음노드를 가리키는 Point 두개의 포인터를 가진다.
트리에서는 부모노드를 가리키는 Point하나만 가지게 된다.
따라서, 공간적 효율성, 포인터 수정에 효율적, Find-Set(x)에서는 비효율적 이게 된다.
1) Make-Set(x)을 한 상태
Make-Set(x): 원소 x로만 이루어진 집합을 만든다.

P[x]는 부모, x는 나를 의미하며 x가 P[x]를 가리키는 것은 부모노드가 나 자신이라는 것을 의미한다.
2) Find-Set(x)을 한 상태
Find-Set(x) : 원소 x를 가지고 있는 집합을 알아낸다.


만약에 x가 대표노드라면 x를 반환해주고, 아니라면 옆의 그림과 같이 재귀적으로 부모노드를 타고
올라가며 대표 노드를 찾는다.
3) Union(x,y)을 한 상태
Union(x,y): 원소 x를 가진 집합과 원소 y를 가진 집합의 합집합을 만든다.

p[Find-Set(y)]으로 나온 집합 Y의 대표노드에 Find-Set(x)의 대표노드를 연결해준다.
즉, 두개의 집합을 합치는 과정이다.
4) 연산의 효율을 높이는 방법
① 랭크를 이용한 Union
각 노드는 자신을 루트로 하는 서브트리의 높이를 랭크Rank 라는 이름을 저장한다.
두집합을 합칠 때 랭크가 낮은 집합을 랭크가 높은 집합에 붙인다.
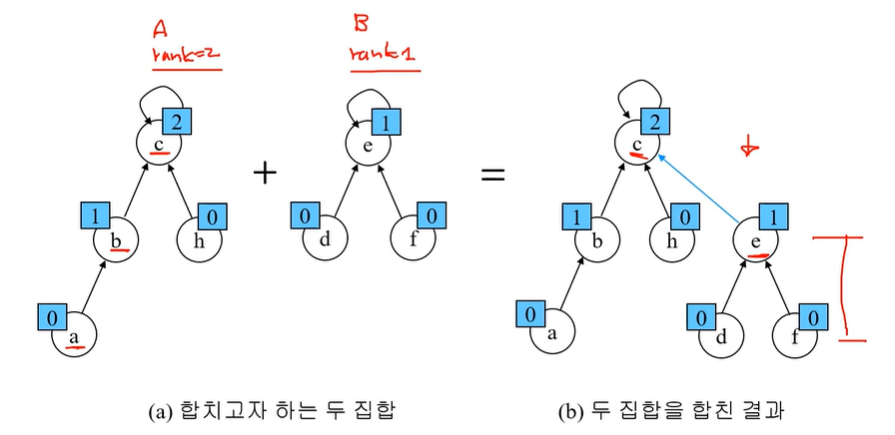
두개의 집합 트리의 깊이가 똑같을 때만, Rank가 증가하게 된다. 다른 경우의 수는 없다.


② 경로 압축
Find-Set(x)을 행하는 과정에서 만나는 모든 노드들이 직접 루트를 가리키도록 포인터를 바꾸어 준다.
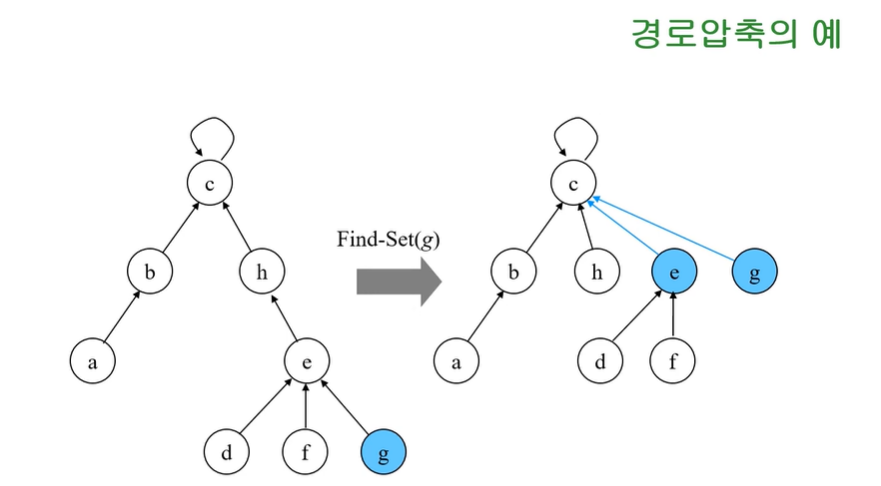
경로 압축은 Find-Set에 내장되어 있다. 쉽게 말해서 Find-Set을 해주는 과정에서 과정 하나만 추가해주면 경로 압축을 할 수 았다. 그 과정이 무엇이냐, 위의 그림을 예시를 들어본다면 Find-Set(g)를 한다고 하자, 그렇다면 트리에서 노드 g를 가리키게 될 것이고, 노드g가 가리키는 부모노드의 포인터를 Root노드로 바꿔주는 것이다. 순서는 이렇다.
1) Find-Set(g)로 노드 g를 찾는다.
2) 노드 g가 가리키는 노드가 Root(대표노드)가 아니라면 대표노드로 연결해준다.
3) Find-Set은 재귀적을 대표노드를 찾아주는 함수이기 때문에, 노드 g에서 대표노드까지 올라가는 과정에
서 만나는 노드들을 전부 대표노드레 다이렉트로 연결해 준다.
Find-Set을 하면 할수록 효율적으로 바뀐다. 또한 Find-Set 과정에 포함되어있기 때문에 각 노드를 대표 노드에 연결하는데 걸리는 수행시간은 O(1)상수시간이다.

5) 수행 시간
트리를 이용해 표현되는 배타적 집합에서 랭크를 이용한 Union과 경로압축을 이용한 Find-Set을 동시에 사용하면, m번의 Make-Set, Union, Find-Set 중 n번이 Make-Set일 때 이들의 수행 시간은 O(mlog*n)이다.
log*n = min{k : log log ...log n<=1} 사실상 선형시간이다.

'Algorithm' 카테고리의 다른 글
| Graph Algorithm(플로이드-워샬 알고리즘) (1) | 2023.03.02 |
|---|---|
| Graph Algorithm(벨만-포드 알고리즘) (0) | 2023.03.01 |
| Graph Algorithm(다익스트라 알고리즘) (0) | 2023.02.24 |
| 최단 경로(Shortest Paths) (1) | 2023.02.24 |
| Union-find Data Structure(연결 리스트를 이용한 처리) (0) | 2023.02.22 |
