벨만-포드(Bellman-Ford) 알고리즘
벨만포드 알고리즘도 그래프에서 최소비용을 구할 수 있는 알고리즘 중에 하나이다. 벨만포드 알고리즘은 최소비용을 구하는 알고리즘 중에서도, 한 정점에서 다른 모든 정점으로 가는데 걸리는 최소비용을 구하는데 사용하는 알고리즘이다. 이 점은 다익스트라와 동일하다. 그런데 벨만포그와 다익스트라 알고리즘 중에서 언제 무엇을 사용해야 하는 걸까?? 그리고 시간 복잡도에서 말하겠지만, 벨만포드 알고리즘은 일반적으로 다익스트라 알고리즘보다 더 시간이 오래 걸리는 탐색 방법인데 굳이 이 방법을 써야할까 ??
우선 벨만포드의 특징 부터 살펴보자 먼저 다익스트라와 마찬가지로 시작점이 존재한다. 하지만 벨만포드의 가장 중요한 포인트는 가중치가 0보다 작을 수 있다는 점이다. 음의 가중치를 허용한다는 얘기이다.
벨만포드의 알고리즘을 쉽게 얘기하자면 간선 1개일 때, 최단경로. 간선 2개일 때, 최단 경로. 간선 3개일 때, 최단경로...쭉쭉 간선을 늘려가면서 간선 |V|-1개일때 최단경로까지 구하는 알고리즘이다.
1. 벨만포드 알고리즘 수도코드 및 알고리즘 원리

①번 반복문 : 첫 번째, 반복문 같은 경우에는 다익스트라와 똑같이 초기에 vertex의 값을 ∞으로 초기화 해주고, 첫번째 값을 0으로 정해줘서 기준을 잡아준다. d=[0, ∞, ∞, ∞ ... ∞]
②번 반복문 : 두 번째, 반복문은 이중반복문으로 되어있는데, 이 의미는 앞에서 말했듯이, edge가 1개 일때, 모든 경우의 수를 보고, 2개 일때, 모든 간선의 경우를 보고 마지막으로 edge가 |v|-1개일 때까지 반복하는 반복문이다.
첫번째 for문이 edge의 개수를 1개부터 |V|-1개 까지 반복해주고, 안에있는 for문이 edge 집합에 있는 U로부터 가는 모든 edge를 고려하는 부분이 되는 것이다.
if(d[u] + w[u, v] < d[v]) then{} 이부분은 다익스트라와 유사한 조건문이다. 마찬가지로 d[u](현재 노드의 값)+w[u,v](현재노드와 다음 가르키는 노드의 간선 가중치의 값)이 d[v](다음 노드) 보다 작은 경우에는
d[v] ← d[u] + w[u, v] 해당 vertex와 weight를 가르키는 다음 vertex의 값으로 update해준다.는 의미이다.
③번 반목문 : 마지막 반복문은 음의 사이클의 존재 여부를 확인해주는 코드이다. 어떻게 존재 여부를 확인 하는냐. 먼저 ②번 반복문이 끝나는 상황에서 edge는 |V|-1개까지 돈 상태이고, ③번 반복문에서 한번더 반복을 하게 되면 edge는 |V|개의 경우의 수까지 본다는 의미이다. 이때, if(d[u] + w[u, v] < d[v]) then{}이 조건문을 다시한번 실행했을 때, 값이 Update가 되면 간선 어딘가에 음의 사이클이 돌고 있다는 의미가 되서 바로 "해가 없음"을 출력하는 것이다. 정상적인 그래프라면 ②번 반복문에서 끝날 것이다.
2. 그림으로 표현한 다익스트라 알고리즘
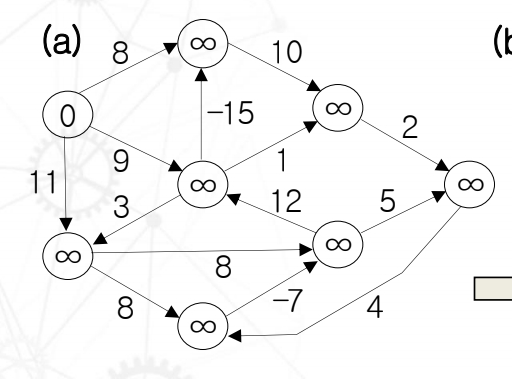
"∞"으로 초기화하고 0으로 r(기준)을 정해준 초기 그래프 모양

Edge가 1개일 때, array는 d=[0, 8, 9, 11, ∞, ∞...∞] 이렇게 된다.
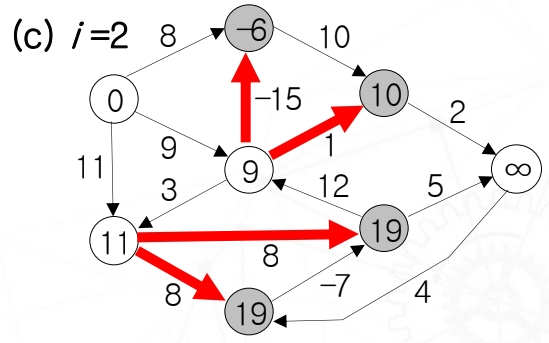
Edge가 2개일 때, relaxation(이완)된 상황이다. edge 1개 사용했을 때는 0 + 8로 vertex 8이였는데 edge 2개를 사용하니깐 0 + 9 - 15로 vertex -6으로 바꾸었다. 나머지는 그대로이고, 똑같이 relaxation해주었다.

Edge가 3개일 때, 지금 relaxation 된 애들은 edge2개로 갈 수 있는 애들이고, 최대 edge를 3개까지 늘려주면서 vertex 12 가 포함되었다.
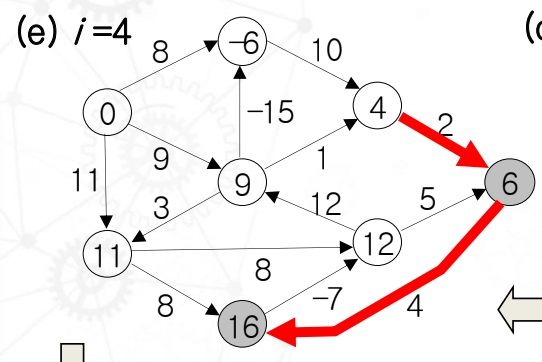
Edge가 4개일 때, vertex 16이 update가 된것을 확인 할 수 있다. 원래는 edge2개일 때도 갈 수 있었지만 vertex 19로 edge 4개를 사용했을 때보다 값이 커서 update했다. edge 4를 시용하면서 거리가 더 짧아 지는것을 볼 수 있다.
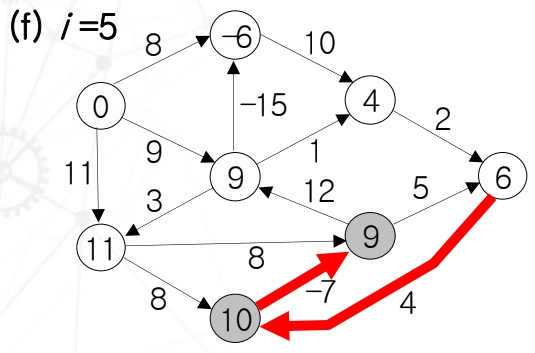
Edge가 5개일 때, 다시한번 update를 해준다.
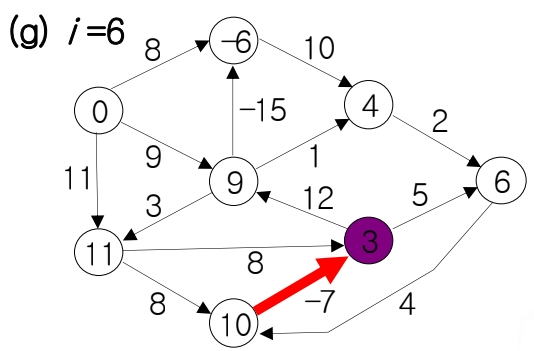
Edge가 6개일 때
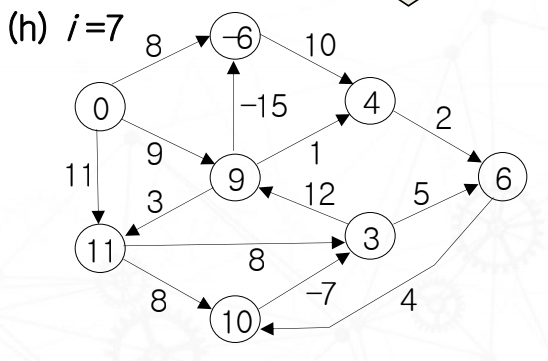
Edge가 7개일 때, 총 vertex가 8개니깐 최대의 간선의 개수 7개까지 보면서 최악의 경우를 계산한다.

위와 같은 과정을 거치면 이러한 최단경로가 나오게 된다.
3. 벨만포드 알고리즘 코드
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
// 간선 구조체
// src = 시작점, dest = 도착점, weight = 가중치
struct Edge
{
int src, dest, weight;
};
// 그래프 구조체
// V :: 정점의 수 E :: 간선의 수
// edge :: 포인터 형식으로 서로 다른 정점을 연결하기 위해 존재
struct Graph
{
int V, E;
struct Edge* edge;
};
// V와 E를 통해 정점과 간선의 수를 가진 그래프를 생성한다.
struct Graph* createGraph(int V, int E)
{
struct Graph* graph = (struct Graph*) malloc(sizeof(struct Graph));
graph->V = V;
graph->E = E;
graph->edge = (struct Edge*) malloc(graph->E * sizeof(struct Edge));
return graph;
}
// 결과를 출력하기 위한 함수
void printArr(int dist[], int n)
{
printf("Vertex Distance from Source\n");
for (int i = 0; i < n; ++i)
dist[i] == INT_MAX ? printf("%d \t\tINF\n", i) : printf("%d \t\t %d\n", i, dist[i]);
}
// src에서 모든 다른 정점까지의 최단 거리를 찾아주는 BellmanFord 함수이다.
// 음의 가중치 까지 적용이 가능하다.
void BellmanFord(struct Graph* graph, int src)
{
int V = graph->V;
int E = graph->E;
int *dist = (int*)malloc(sizeof(int)*V); // int dist[V+1]과 같다.
// 모든 최단 거리를 무한대로 지정해주고, 시작점(src)만 0으로 초기화 한다.
for (int i = 0; i < V; i++)
dist[i] = INT_MAX;
dist[src] = 0;
// 벨만 포드 알고리즘
for (int i = 1; i <= V - 1; i++)
{
for (int j = 0; j < E; j++)
{
int u = graph->edge[j].src;
int v = graph->edge[j].dest;
int weight = graph->edge[j].weight;
// 정점u가(시작점이) 무한대가 아니고,
// 시작점까지의 최단 거리 + 가중치가 도착점의 가중치
// 보다 작을 때 업데이트 해준다.
if (dist[u] != INT_MAX && dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
// 음의 가중치 때문에 무한히 최단 경로가 작아지는 것이 있다면
// 탐색하여 알려준다.
for (int i = 0; i < E; i++)
{
int u = graph->edge[i].src;
int v = graph->edge[i].dest;
int weight = graph->edge[i].weight;
// if문에서 현재위치 최단거리 + 가중치가 계속해서 더 작아질 경우
// 음의 사이클이 있다고 판단한다.
if (dist[u] != INT_MAX && dist[u] + weight < dist[v])
printf("Graph contains negative weight cycle\n");
}
printArr(dist, V);
return;
}
int main()
{
int V = 5; // 정점의 수
int E = 9; // 간선의 수
struct Graph* graph = createGraph(V, E);
// 그래프 정보를 입력해준다.
graph->edge[0].src = 0; // 0에서
graph->edge[0].dest = 2; // 2로 가는 간선의
graph->edge[0].weight = 1; // 가중치는 1로 정한다.
graph->edge[1].src = 0;
graph->edge[1].dest = 3;
graph->edge[1].weight = 5;
graph->edge[2].src = 1;
graph->edge[2].dest = 2;
graph->edge[2].weight = -2;
graph->edge[3].src = 2;
graph->edge[3].dest = 1;
graph->edge[3].weight = 4;
graph->edge[4].src = 2;
graph->edge[4].dest = 3;
graph->edge[4].weight = 4;
graph->edge[5].src = 3;
graph->edge[5].dest = 0;
graph->edge[5].weight = -1;
graph->edge[6].src = 3;
graph->edge[6].dest = 1;
graph->edge[6].weight = 3;
graph->edge[7].src = 4;
graph->edge[7].dest = 0;
graph->edge[7].weight = 1;
graph->edge[8].src = 4;
graph->edge[8].dest = 2;
graph->edge[8].weight = -1;
BellmanFord(graph, 0);
return 0;
}
'Algorithm' 카테고리의 다른 글
| 알고리즘 Introduction & Analysis (0) | 2023.07.08 |
|---|---|
| Graph Algorithm(플로이드-워샬 알고리즘) (1) | 2023.03.02 |
| Graph Algorithm(다익스트라 알고리즘) (0) | 2023.02.24 |
| 최단 경로(Shortest Paths) (1) | 2023.02.24 |
| Union-find Data Structure(트리를 이용한 처리) (0) | 2023.02.22 |
