Introduction
알고리즘 (Algorithm)
※ 주어진 일(또는 문제)을 처리하여 원하는 결과(output)를 얻기까지의 과정을 명확하고 단계적으로 서술한 것
예)
- 조리법 : 음식을 만드는 알고리즘
- 길안내 : 낯선 도시에서 길을 찾아가기 위한 알고리즘
- 세탁기조작법 : 세탁기 조작을 위한 알고리즘
- 악보 : 음악연주를 위한 알고리즘
※ 알고리즘을 찾는 작업의 효시
- 현대의 컴퓨터가 개발되기 훨씬 전부터 수학의 한 분야로 시작
※ 목표
- 특정 유형의 모든 문제들을 해결할 수 있는 방법을 서술하는 일련의 명령들을 찾는 것
※ 알고리즘의 예 : 유클리디안 알고리즘(Euclidean algorithm)
- 그리스 수학자 유클리드가 발견함
※ 일단 작업을 수행하기 위한 알고리즘을 찾은 다음에는 알고리즘이 기초하고 있는
원리에 대한 이해는 더 이상 작업수행에 필요하지 않다.
- 각 알고리즘에 대한 이해 없이도, 최대고약수를 찾기 위해 호제법 알고리즘을 따라 할 수 있다.
- 어떤 의미에서는 해당 문제의 해결을 위해 요구되는 지능이 알고리즘 안에 인코딩 되어 있다고 볼 수 있다.
※ 따라서, 알고리즘이 주어지면 누구든 그 일을 할 수 있다.
- 유용한 작업을 수행하는 컴푸터를 만들 수 있는 것은 알고리즘에 지능을 담아 전달하는 방식을 사용하기 떄문이다.
※ 특정 문제에 대해 여러 알고리즘이 있을 수 있다.
※ 효율적인 알고리즘을 개발해서 사용하는 것이 바람직하다.
- 시간 효율성(실행 시간을 빠르게)
- 공간적 효율성(메모리 사용을 적게)
Algoruthm for Computer Program
※ 프로그램(Program)
- 알고리즘의 표현 형식 중 하나
- 알고리즘을 컴퓨터가 이해 가능하게 표현하여 구현한 것
- 프로그램은 알고리즘을 프로그래밍 언어로 나타낸 것
- 컴퓨터가 처리할 일을 순차적으로 기술한 일련의 명령문(instruction)
- 명령문 : cpu가 처리하는 단일 작업(operation)
※ 프로그래밍(Programming)
- 프로그램을 개발하는 과정
- 코딩 + 분석 및 구현 + 디버깅 + 컴파일 + 테스팅 등등
- 프로그램을 컴푸터가 처리할 수 있는 형식으로 인코딩하여 컴퓨터 안에 저장시키는 과정
※ 코딩(Coding)
- 알고리즘을 특정한 프로그래밍 언어로 변환하여 작성하는 것
- 한 언어에서 다른 언어로 코드를 만드는 과정을 의미
※ 컴퓨터과학 : 알고리즘에 관한 학문
※ 컴퓨터과학의 범위 : 다른 분야의 학문적 성과들을 응용한 다양한 주제
※ 컴퓨터과학 기술의 영향력
Motivation
Algorithms
※ 알고리즘(Algorithm)이란?
- 어떤 문제를 풀기 위한 유한한 절차와 방법
- 여기서 문제는 보통 '수학적으로 엄밀히' 정의된 문제에 한정됨
※ 절차와 방법?
- 계산 문제를 풀기 위해서는? : 숫자와 사칙연산을 이용
- 컴퓨터로 계산 문제를 풀기 위해서는? : 컴퓨터에 주어진 명령어 집합(instruction set)을 이용
Example of Algorithm
문제:
- n 정수로 구성된 리스트에 S에 정수 x가 있는가?
입력:
- 양의 정수 n, 첨자 1에서 n까지 구성된 정수 목록 S, 정수 x
출력:
- location: x가 존재하는 리스트 S의 첨자, x가 S가 존재하지 않으면 0
알고리즘:
void Algorithm1(int n, const int S[], int x, index &location)
{
location = 1;
while(location <= n && S[location] != x)
location ++;
if(location > n)
location = 0;
}
//의사코드(Psedo-code):
- 알고리즘으로 수행할 절차를 다양한 언어로 간략하게 서술해 놓은 것
Analysis of Algorithm
알고리즘의 성능을 분석하는 방법
1. 실험적 분석(Experimental analysis)
- 주어진 알고리즘을 소스코드로 구현한 다음, 실제 환경에서 동작시켜 실행 시간을 측정
ex) c언어에서는 clock() 이라는 함수를 이용해서 알고리즘의 동작 시간을 측정 가능
※ 실험적 분석의 문제점
- 알고리즘을 실제 구현하기까지 시간과 노력이 소모
- 두 알고리즘의 성능을 비교할 때, 기본적으로 명시된 것들(하드웨어 사양) 및 측정할 수 없는
- 다양한 외부 요인들로 인해 정확한 비교가 힘듦
2. 이론적 분석(Theoretical analysis) ---//알고리즘 과목에서 주로 사용할 방법
- 알고리즘 수행 시간(=성능)을 실제로 구현을 통해서가 아닌, high-level에서 이론적으로 기술하는 방법
- 시간은 보통 입력 사이즈(보통 n으로 표기)에 관한 함수로 표현됨
- 사용하는 하드웨어 및 소프트웨어와 무관하게 알고리즘의 성능을 표현 가능
- 이론적 분석을 통해 구한 알고리즘 수행시간을 시간 복잡도(time complexity)
※ 이론적 분석에서 고려하는 기본 연산들
- 숫자를 변수에 대입
- 함수를 호출, 함수의 결과값을 반환
- 두(작은) 정수 사이의 사칙 연산
- Array의 Get, Set 연산
- 기타 컴퓨터 하드웨어에서 정의 된 단일 명령어
※ 위의 각각의 연산들이 걸리는 시간은 하드웨어 및 소프트웨어와 관계가 있으므로 정확한 시간은 알 수 없음
※ 하지만 각각의 단일 연산들은 입력 크기와 무관하다는 것을 알 수 있음
※ 이 경우 이론적으로 이 연산들은 상수 시간(constant time)이 소모 된다고 함.
Analysis of Algorithm
문제:
- n 정수로 구성된 리스트에 S에 정수 x가 있는가?
입력:
- 양의 정수 n, 첨자 1에서 n까지 구성된 정수 목록 S, 정수 x
출력:
- location: x가 존재하는 리스트 S의 첨자, x가 S가 존재하지 않으면 0
알고리즘:
void Algorithm1(int n, const int S[], int x, index &location)
{
location = 1; <---------- 1
while(location <= n && S[location] != x) <---------- n
location ++; <---------- 1
if(location > n) <---------- 1
location = 0; <---------- 1
}
문제:
- n 정수로 구성된 리스트에 S에 숫자를 더해라
입력:
- 양의 정수 n, 첨자 1에서 n까지 구성된 정수 목록 S
출력:
- sum : 리스트S에 있는 n개의 정수들의 합 첨자
알고리즘:
number Algorithm2(int n, const int S[])
{
index i; <---------- 0
number result = 0; <---------- 1
for(i = 1; i <=n; i++) <---------- n
result = result + S[i]; <---------- 1
return result; <---------- 1
}
문제:
- n 정수로 구성된 리스트 S를 단조감소 순서로 나열하라
입력:
- 양의 정수 n, 첨자 1에서 n까지 구성된 정수 목록 S
출력:
- S: 단조감소 순서로 나열된 리스트
알고리즘:
void Algorithm3(int n, int S[])
{
index i,j; <---------- 0
for(i = 1; i <= n; i++) <---------- n
for(j = i + 1; j<=n; j++) <---------- n-i
if(S[j] < S[i]) <---------- 1
S[i]와 S[j]를 교환하라 <---------- 1
}
Data Structure & Algorithm
※ 자료구조는?
- 그릇(자료)을 효율적으로 관리하는 방법
※ 알고리즘은?
- 목적지까지 최적의 이동 경로를 찾는 방법
Expression of Algorithm
알고리즘 표현법
※ 일반 언어 표현
- 일반적인 자연어를 사용해서 설명하듯이 알고리즘을 표현
- 일반 사람이 이해하기 쉽게 표현할 수 있으나, 최종적으로 코드로 변 경하는 데는 한계가 있음
- 어떤 알고리즘을 사용해야 할지 아이디어가 떠오르지 않는 시점에서, 생각 범위를 넓히는 단계 정도에 사용하면 무난
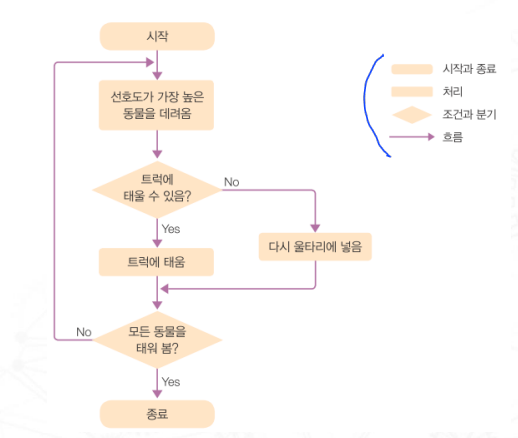
※ 순서도를 이용한 표현
- 여러 종류의 상자와 상자를 이어 주는 화살표를 이용해서 명령 순서 를 표현
- 간단한 알고리즘은 쉽게 표현할 수 있지만, 복잡한 알고리즘은 표현 하기 어려운 경우가 많음
※ 의사코드를 이용한 표현
- 프로그래밍 언어보다는 좀 더 인간의 언어에 가까운 형태
- 프로그램 코드와 일반 언어의 중간 형태
- 프로그램 코드를 직접 코딩하는 것보다 알고리즘을 좀 더 명확하게 정립하는 데 도움이 되고
- 코드에 설명을 달지 않아도 이해하는데 무리없음

※ 프로그램 코드로 표현
- 실제로 사용하는 프로그래밍 언어의 코드로 바로 작성 가능
Evaluation of Algorithm
알고리즘의 성능
※ 알고리즘 성능 표기
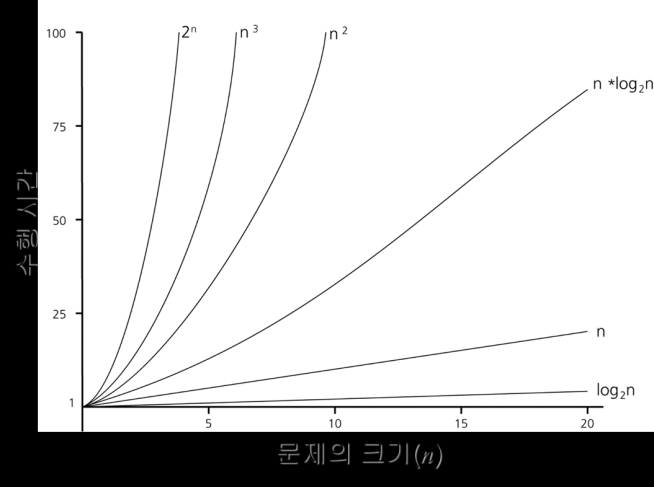
- 빅-오 표기법(Big–Oh Notation)으로 O(f(n)) 형태
- 대표적인 함수는 O(1), O(log n), O(n), O(n log n), O(n2 ), O(n3 ), O(2n ) 정도가 있다.
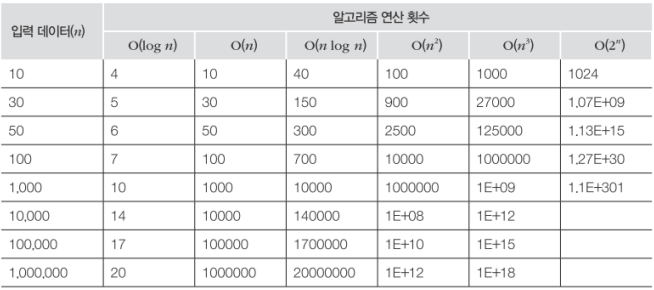
Big-Oh notation
※ Big-Oh notation (Big-Oh 표기법)
- 이론적 분석에서는 걸리는 시간을 표현한 함수 자체보다 입력 사이즈에 비 례해서 해당 함수가 어느 정도로 증가하는가에 더 관심이 많음 (예: 입력이 10배 커지면 시간은 얼마나 늘어 날까?).
- 앞선 constant time 연산들은 입력 사이즈와 무관


O(1) - (상수) Constant
- 입력되는 데이터양과 상관없이 일정한 실행 시간을 가진다.
- 알고리즘이 문제를 해결하는데 오직 한 단계만 거친다.
O(logN) Logarithmic
- 데이터양이 많아져도, 시간이 조금씩 늘어난다.
- 시간에 비례하여, 탐색 가능한 데이터양이 2의 n승이 된다.
- 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어든다.
- 만약 입력 자료의 수에 따라 실행 시간이 이 log N 의 관계를 만족한다면 N이 증가함에 따라 실행 시간이 조금씩 늘어난다. 이 유형은 주로 커다란 문제를 일정한 크기를 갖는 작은 문제로 쪼갤때 나타나는 유형이다.
Binary Search • O(N) Linear
- 데이터양에 따라 시간이 정비례한다.
- linear search, for 문을 통한 탐색을 생각하면 되겠다.
O(N log N) log linear
- 데이터양이 N배 많이 진다면, 실행 시간은 N배 보다 조금더 많아 진다. (정비례 하지 않는다.)
- 이 유형은 커다란 문제를 독립적인 작은 문제로 쪼개어 각각에 대해 독립적으로 해결하고,나중 에 다시 그것들을 하나로 모으는 경우에 나타난다. N이 두배로 늘어나면 실행 시간은 2배보다 약 간 더 많이 늘어난다.
- 퀵소트, 머지소트
O(N2 ) Quadratic
- 데이터양에 따라 걸리는 시간은 제곱에 비례한다. (효율이 좋지 않음, 사용하면 안된다)
- 이 유형은 이중루프내에서 입력 자료를 처리 하는 경우에 나타난다. N값이 큰값이 되면 실행 시 간은 감당하지 못할 정도로 커지게 된다.
- 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱
- 2중 for 문을 사용하는 버블소트, 삽입정렬(insertion sort)
'Algorithm' 카테고리의 다른 글
| 병합정렬(MergeSort) (2) | 2023.07.23 |
|---|---|
| 퀵정렬(QuickSort) (1) | 2023.07.23 |
| Graph Algorithm(플로이드-워샬 알고리즘) (1) | 2023.03.02 |
| Graph Algorithm(벨만-포드 알고리즘) (0) | 2023.03.01 |
| Graph Algorithm(다익스트라 알고리즘) (0) | 2023.02.24 |
